About

I am a research fellow (chargé de recherche) in the HeKA Inria team hosted at PariSanté Campus. Prior to that, I did my PhD under the supervision of Alain Trouvé at the ENS Paris-Saclay and worked as a PostDoc at Imperial College London in the team of Michael Bronstein. Here is a short CV.

I am primarily interested in geometry - from computer graphics to Riemannian manifold embeddings - with a focus on medical applications. With a group of close collaborators, my work focuses on:

• Geometric data analysis: graph- and measure-theoretic methods to study large datasets.
  We develop the KeOps library to accelerate computations on distance- and kernel-like matrices.
• Optimal transport theory: generalized sorting algorithms in dimension D > 1.
  We develop the GeomLoss library that provides the fastest solvers available for dicrete optimal transport.
• Computational anatomy: shape analysis for medical imaging and biology.
  We have recently launched the shape seminar (YouTube) and the scikit-shapes library.

Contact:

• E-mail: name.surname@inria.fr.
• Address: Office 3.14 (π), Équipe Inria HeKA, PariSanté Campus,
  2 - 10 Rue d'Oradour-sur-Glane, 75015 Paris. Métro Balard or Porte de Versailles.

Team, students and close collaborators:

• Antoine Poirot-Bourdain (engineer, with Emmanuel Bacry and Anne-Sophie Jannot, 2023-28), survival analysis on national insurance data, with GPUs.
• Guillaume Houry (PhD student, with François-Xavier Vialard, 2024-27), optimal transport and bone fractures.
• Robin Magnet (PostDoc, 2024-27), functional maps and bone fractures.
• Louis Goldenberg (Industry PhD student at Dassault Systèmes, with Eloi Mehr, 2024-27), cardiac anatomy.
• Hadrien Bigo-Balland (CIFRE PhD student at MyFit Solutions, with Jérémy Adoux and Maxime Bodier, 2023-26), anatomy from 3D scans acquired with a smartphone.
• Eya Abid (PhD student, with Slavica Jonic, 2023-26), estimation of protein conformation manifolds from Cryo-EM data.
• Guillaume Sérieys (PhD student, with Joan Glaunès and Pietro Gori, 2022-25), metamorphoses in shape analysis.

Alumni:

• Ivan Lerner (medical doctor, PhD student, informal supervision, 2021-24), Gaussian processes for electronic health records. Now public health doctor at Hôpital Européen Georges-Pompidou and AHU in the HeKA team.
• Tom Boeken (medical doctor, PhD student, informal supervision, 2021-24), computational anatomy for interventional radiology. Now interventional radiologist at Hôpital Européen Georges-Pompidou and MCU-PH in the HeKA team.
• Louis Pujol (engineer, with Stéphanie Allassonnière, 2023-24), scikit-shapes. Now research engineer at Dassault Systèmes.
• Alexis Van Straaten (engineer, with Anne-Sophie Jannot, 2022-23), survivalGPU.

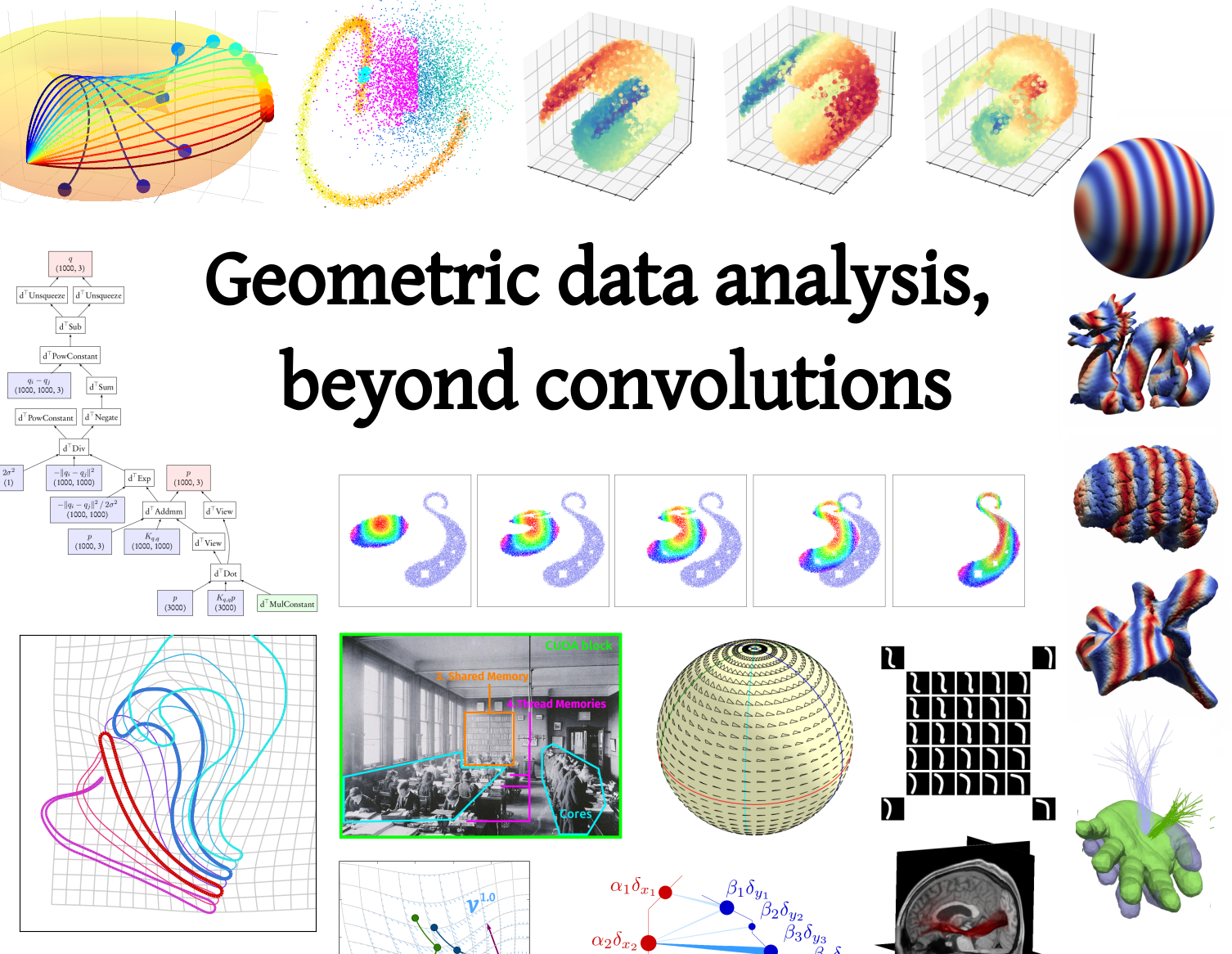
July 2020: Geometric data analyis, beyond convolutions

I defended my PhD thesis on July 2nd, 2020: a related video recording is available here. My thesis is the best introduction to my work: it is written as a textbook for data sciences and shape analysis, from a geometric perspective. If you just saw one of my talks on symbolic matrices, geometric learning and large-scale optimal transport, here is what you are looking for: KeOps library, GeomLoss package, Slides for the defense, PhD thesis.

Miscellaneous

My wife Anna is doing inspiring work on 3D shape textures. Check it out!

I played the flute for 11 years at the Conservatoire Paul Dukas, in Paris. I especially enjoy playing baroque music: J.S. & C.P.E. Bach, J.J. Quantz, G.P. Telemann... I gratuated from the Conservatoire in June 2014, obtaining a "Certificat de Fin d'Études Musicales" diploma (Mathematics in Music). I am currently learning how to play the balalaika - check out this fantastic piece by Alexey Arkhipovsky to understand why!

My other interests include ancient history, Chinese culture and pedagogy. Here are some books, blogs and videos that I would strongly recommend:

• Oliver Byrne's "Elements of Euclid": a pedagogical masterpiece.
• Thucydide's history of the Peloponnesian war, a thrilling mix of adventure and wisdom.
• Historia Civilis, the unexpected encounter of the two points above!
• Bret Devereaux's blog on history and popular culture, a brilliant read every Friday.
• Chaos and Dimensions, two movies by Jos Leys, Aurélien Alvarez and Étienne Ghys. A must-see for anyone interested in math!
• Faraday's chemical history of a candle, explained by Bill Hammack, the engineerguy.
• Branch Education's YouTube channel. Clear, concise and illuminating videos on the inner workings of modern computer hardware.
• Topology from the differentiable viewpoint by John Milnor: a concise and elegant introduction to differential topology. Everything — including Brouwer fixed point theorem and Hopf theorem — is deduced from the single fact that a smooth and compact 1-manifold has an even number of extremal points!
• Hyperbolic geometry by J.W. Cannon: includes a proof of the usual properties of the Poincaré half-plane... without a single calculation, but stereographic projections and symmetries instead.