Geometric data analysis (MVA) — AI for healthcare (Epita)

Since October 2022, I teach a class on geometric data analysis in the MVA program. I also used the same material in the Epita school of engineering and computer science (healthcare major).
MVA lectures take place on Friday afternoons (2pm-5pm) in the Dieulafoy lecture hall (map) of the Cochin campus of the Faculté de Médecine (Chaire IA Santé), 27 rue du Faubourg Saint-Jacques (Port-Royal on the RER B line). An up-to-date schedule is available here.

Teaching materials. Video recordings and slides for all lectures are available below:

1. Introduction: Video, MVA, Epita, Latex.
2. Flat vector spaces: Video, MVA, Epita, Latex. Lab: scikit-learn classifiers.
3. Graphs and embeddings: Video, MVA, Epita, Latex. Lab: UMAP on penguins, mammoths and integers.
4. Geometric deep learning: Video, MVA, Epita, Latex. Lab: first steps with PyG.
5. Riemannian metrics and geodesics: Video, MVA, Latex. Lab: first steps with GeomStats.
6. Probability distributions: Video, MVA, Latex. Lab: gradient flows with GeomLoss, deeper dive and code.
7. GPU programming: Video, MVA, Latex.

Validation. Please note that our classroom is located in downtown Paris, more than one hour away from the ENS Paris-Saclay. In this context, attendance is not mandatory to validate the class. If you cannot attend the lectures in-person, please send me an e-mail (name.surname@inria.fr) and follow the guidelines below:

• PhD students who need an administrative "stamp": presence in 4 out of 7 lectures or a two-page-long essay on your main takeaways from the class and its applications to your work. Please register to the mailing list to receive important information about the class.
• M2 students (MVA, MASH, etc.): quiz + project. More precisely:
  • Please register to the mailing list to receive important information about the class.
  • A list of project suggestions is available here. It contains precise information about my grading scale.
  • I expect a 4-8 pages PDF report, written using the two-columns Siggraph template for Latex. An example PDF file, with a .zip template.
  • Groups of 2-3 students are encouraged. Solo projects are not allowed, barring exceptional circumstances.
  • Shared projects with other lectures are not allowed by the MVA program.
  • Project reports are due on Wednesday, the 4th of December 2024. If you send your report late, every day after the deadline will cost you a "minus 2 points" penalty.
  • Project presentations will take place between Monday, the 9th of December and Friday, the 13th of December 2024. Presentations will be via Zoom: 10mn + questions.
  • A short exam will take place on Wednesday, the 18th of December 2024. This will be an online quiz, to be filled in 30mn; you may start the exam at any time of the day.

Going further. I am working on full lecture notes for the class. You may also be interested by the following references:

• Tom Fletcher’s lecture notes on the geometry of data
• The textbook on Riemannian geometric statistics in medical image analysis.
• Justin Solomon’s lecture notes on shape analysis.
• Cem Yuksel's lectures on introduction to computer graphics and interactive computer graphics.
• Gabriel Peyré and Marco Cuturi’s textbook on computational optimal transport.
• Keenan Crane’s lecture notes on discrete differential geometry.
• Michael Bronstein, Joan Bruna, Taco Cohen and Petar Veličković's textbook on geometric deep learning.
• My PhD thesis, "Geometric data analysis, beyond convolutions"".
• Some of these cool links.

"Artificial Intelligence" for radiologists

Since June 2018, I have been speaking in several radiology events to demystify image processing algorithms and engage fruitful discussions between researchers and physicians. My up-to-date slides on the subject are available here and there in French, and at this address in English. You may be interested by these two video recordings, in French: a general introduction to medical imaging and a detailed presentation on neural networks.

I'm also in charge of the "Shape/Image Processing" workshop session at the AI-Radiology Masterclass, targeted at radiology interns and organized by the Paris Descartes University since February 2019. The full Python notebooks are available here, and pre-rendered versions can be accessed through the following links:

• Introduction to image processing.
• Subsampling, masking and convolutions.
• Segmentation of an aorta with five lines of code.
• Doing geometry with point clouds.
• Register shapes through gradient descent.
• Fourier analysis, the JPEG standard.
• Wavelet analysis, the JPEG2000 standard.

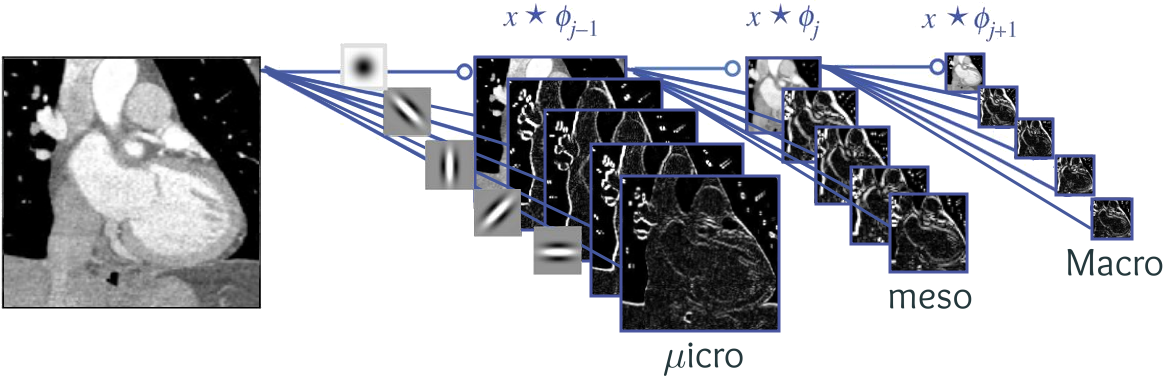
Data Sciences workshop sessions

I was in charge of the workshop sessions for the course of Gabriel Peyré, "Mathematical Foundations of Data Sciences".

My workshop notes are available here.

In the sessions 11-12, we present supervised learning methods from a geometric point of view. The full Python notebooks are available here, and you can read the pre-run versions by clicking on the links below. If you have a mathematical background, these files could help you to get a hands on experience of "neural networks" and "deep learning" methods.

• Introduction to supervised machine learning.
• Building Convolutional Neural Networks - part I.
• Building Convolutional Neural Networks - part II.
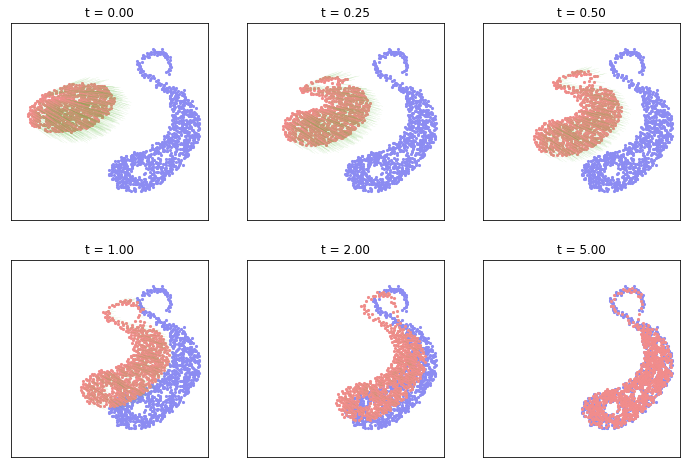
• Gradient flows between sampled measures.
• Fitting a generative model.

In the last session, we present Riemannian methods for shape analysis. The full Python notebooks (that I initially prepared for the GeomData summer school) are available here, and you can read the pre-run versions by clicking on the links below. If you have a math or CS background, these files could help you to get a first introduction to the geometric theory of shapes spaces.

• Introducing Kendall's sphere of triangles.
• Tangent PCA on a Riemannian manifold.
• Statistical study of a population of worms.
• Working with unlabeled shapes.
• Geodesic shooting on a shapes space.

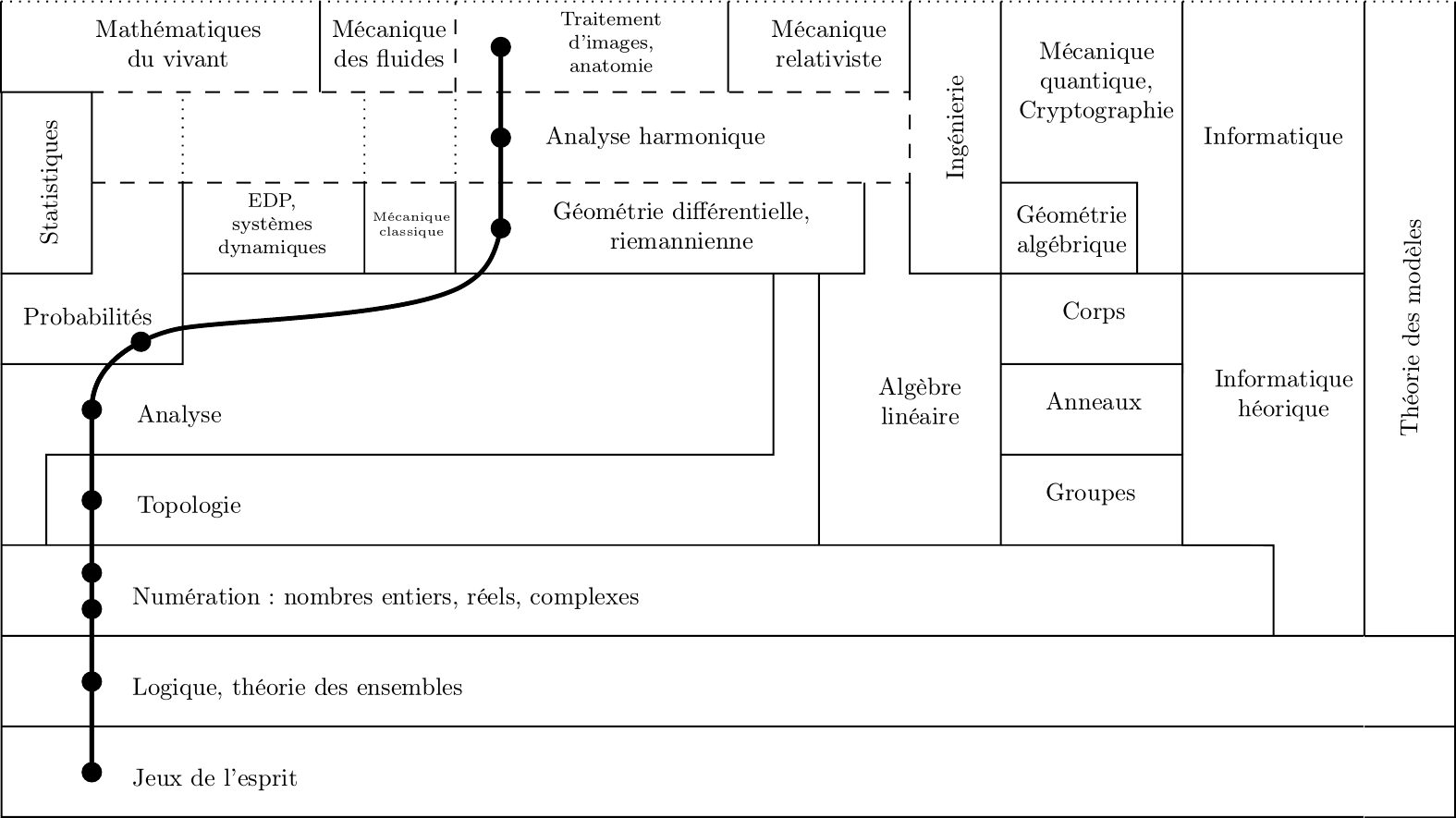
Culture mathématique : Fondations, Analyse, Géométrie

Ce cours est destiné aux élèves de l'ENS désireux d'avoir une idée juste de ce que sont les mathématiques, vues par les mathématiciens. Plutôt que de donner un panorama de thèmes célèbres, on y met en avant les qualités essentielles à cette science : rigueur bien sûr, mais surtout capacité à "abstraire", c'est à dire à identifier dans des problèmes apparemment éloignés une structure commune.

Le cours convient aussi bien aux élèves des départements littéraires qu'aux élèves des départements de sciences sociales ou de sciences dures : plus qu'un contenu technique, il s'agit de faire découvrir une manière d'analyser le monde qui nous entoure.

Le cours s’articule en deux temps :

• 1) Complexes et géométrie :
  • Pourquoi démontrer plusieurs fois un même résultat ?
  • Des épicycles de Ptolémée au format '.jpg', l'analyse harmonique.
  • Faire de la géométrie sur des espaces courbes...
  • Dont la sphère des triangles, et ses applications surprenante en archéologie !
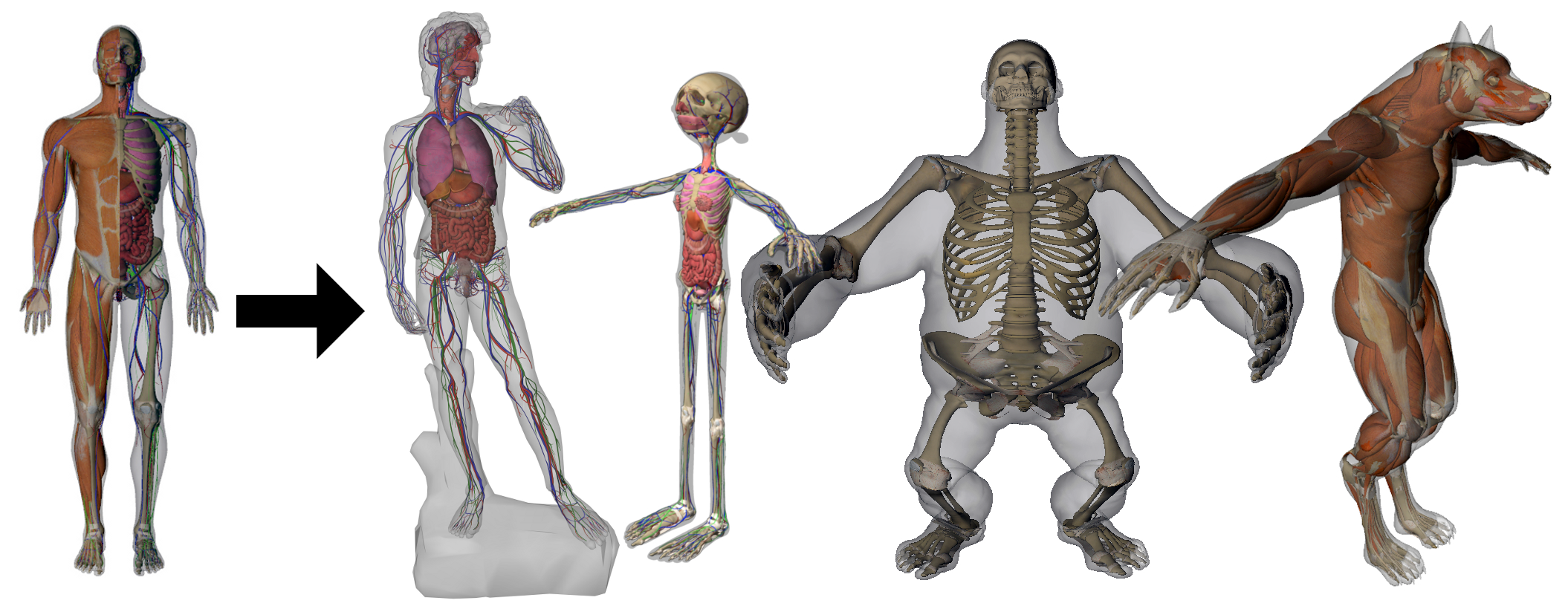
  • Espaces de formes et avenir de l'anatomie médicale.
• 2) Fondements de la logique, numération, analyse :
  • Ce fameux Gödel, que dit-il au juste ?
  • Pourquoi les nombres réels ? Complexes ?
  • Pour un mathématicien d'aujourd'hui, qu'est-ce-qu'une dérivée ?
  • Et d'ailleurs, comment simule-t-on un avion en soufflerie ?

Ce cours est particulièrement adapté aux élèves s'intéressant à l'histoire et à la philosophie des sciences, ou plus généralement à tous ceux désireux de se forger une culture scientifique avancée. C'est aussi l'occasion de mieux comprendre ce sur quoi travaillent vos amis matheux !

N.B. : Pour tirer pleinement profit des portions les plus techniques du cours, des souvenirs de terminale S sont nécessaires - disons, une exposition préalable aux notions de dérivée et de nombre complexe.

Une version courante des notes de cours - que je vous invite à feuilleter - est accessible ici.

Je travaille pour aboutir à un manuel destiné aux enseignants du secondaire, et espère ainsi pouvoir leur proposer un contenu neuf, proche des préoccupations des chercheurs avec de véritables ouvertures sur des problèmes appliqués.

Introduction à la géométrie riemannienne par l'étude des espaces de formes

Pour les mois d'automne-hiver 2016 et 2018, j'ai la chance d'encadrer onze élèves de première année pour une lecture en groupe du manuel de géométrie riemannienne de John M. Lee, An Introduction to Curvature, assorti d'une poignée d'articles liés à la théorie des espaces de formes. Semaine après semaine, nous avons écrit ensemble un petit polycopié, que l'on peut utiliser comme porte d'entrée à la théorie des espaces de formes.

Colles et classes prépa'

Voici quelques exercices (corrigés) donnés à l'occasion de colles en MPSI2 et MP* au lycée Marcelin Berthelot. J'ai trouvé plus simple de faire les dessins à la main... Les fichiers sont donc un peu lourds.

• Suites numériques : une suite bornée dont aucune moyenne de Cesàro ne converge : corrigé - appendice
• Analyse de fonctions : le théorème de Darboux : partie 1 - partie 2
• Analyse et Topologie : les polygones réguliers minimisent l'aire et le périmètre : partie 1 - partie 2 - partie 3
• Combinatoire infinie : il y a autant de fonctions continues que de réels corrigé
• Analyse : une fonction convexe est dérivable sauf en un nombre dénombrable de points : corrigé

Pour les Spé qui s'ennuient pendant les vacances, voici deux polycopiés de cours, donnés à l'ENS, qui pourraient vous intéresser : Analyse complexe et harmonique, par Wendelin Werner : les séries entières vues par un géomètre/physicien; Traitement du Signal, par Stéphane Mallat : l'analyse de Fourier de manière ludique et amusante (vous y apprendrez notamment comment fonctionne le format JPEG).